After this lesson, students will know how to organize information into a probability tree or tree diagram. They will understand how to read tree diagrams and how they relate to compound probabilities. They will understand when to multiply probabilities and when to add probabilities.
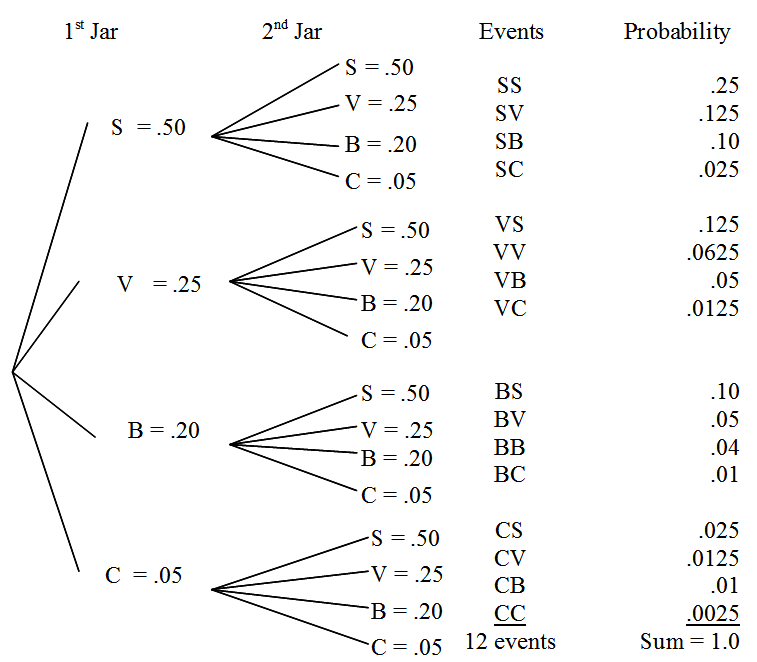
“Remember the problem with the candy jar on the principal’s desk? Today we are going to learn how we can organize that information into a tree diagram. Recall that there were 10 strawberry candies, 5 vanilla, 4 blueberry, and 1 chocolate in each jar. [IS.4 - Struggling Learners] What is the probability of each flavor?” [10/20 = 1/2, 5/20 = 1/4, 4/20 = 1/5, 1/20]
“What do all of the probabilities add up to?” (1)
(Note: What you pick in the first jar does not affect what you pick in the second jar.)
Have students record the following tree diagram in their notes.
“This is an example of a tree diagram. [IS.5 - All Students] Each branch represents the possible events along with the probability of each event. The branches add up to a probability of 1. The first four branches represent picking a candy from the jar and the second set of branches represent picking another candy from the jar. The events and probabilities on the right represent the intersection of the two branches. You multiply across, [IS.6 - Struggling Learners] but if you wanted to know the probability of getting at least one strawberry, you add up all the events that have an S in it.” [.25 + .125 + .10 + .025 + .125 + .10 + .025 = .775]
-
“This tree diagram represents two independent events. But what if the principal let you pick two candies? If you picked a strawberry first, what is the probability of picking a strawberry on the second pick?”
(You picked a strawberry first, so now there are only 9 strawberries left and the total is now at 19 or 9/19 = .474)
“What is the probability of picking 2 strawberry candies from one jar?”
-
[ 10/20 × 9/19 = .50 × .474 = .237]
“This ‘without replacement’ situation means the second pick is dependent on the first. If this was a ‘with replacement’ situation and you had picked a candy and then put it back, the results of the second pick would have been independent of the first.”
- The Fundamental Counting Principle states that if there are a ways to do one thing and b ways to do another, then there are a•b ways to do both things. For example, if someone has 3 different color t-shirts and 2 different color shorts, then there are 3 × 2 = 6 ways to choose one t-shirt and one pair of shorts.
Activity 1: Think-Pair-Share
Write on the board or distribute to students the following problem to think about on their own, and then pair students to answer the questions. [IS.7 - All Students] When everyone has completed the problem, have the pairs share their findings with the class.
“In basketball, a player gets to shoot two free-throws if s/he is fouled during his/her shot and the shot does not go in the basket. Melanie makes her free-throws 6 times out of 10 attempts. The sample space is a listing of all possible outcomes of the event.”
-
What are all the possible outcomes of her two shots?
-
[(make, make); (make, miss); (miss, make); (miss, miss) These are the outcomes that make up the sample space.]
-
Find the following probabilities:
-
P(make, make) = (0.6 × 0.6 = 0.36)
-
P(make, miss) = (0.6 × 0.4 = 0.24)
-
P(miss, make) = (0.4 × 0.6 = 0.24)
-
P(miss, miss) = (0.4 × 0.4 = 0.16)
-
What is the probability of her making at least one shot?
-
(0.36 + 0.24 + 0.24 = 0.84)
-
What is the probability of her two shots being the same (meaning make-make or miss-miss)? (0.36 + 0.16 = 0.52)
Activity 2: Groups
Divide the class into groups of 4 and provide students the following problem to work on. [IS.8- All Students]
“You are at an ice cream parlor that only serves the two most popular flavors: chocolate and vanilla. You may take as many scoops of each flavor as you want per serving. You choose chocolate 8 out of 10 visits.”
-
1. Write out all the possibilities for choosing an ice cream cone with 3 scoops.
CCC CCV CVC VCC
VVV VVC VCV CVV
-
2. What is the probability that you get a cone with at least one scoop of vanilla? [7/8 = 0.875]
-
3. What is the probability that you get a cone with exactly two scoops of chocolate? [3/8 = 0.375]
-
4. What is the probability that you get a cone with all the same flavor? [2/8 = 0.25]
-
5. What is the probability that you get a scoop of chocolate on the third scoop, given you got a scoop of vanilla on the first scoop? [2/8 = 0.25]
-
6. One day per month, the ice cream parlor sells another flavor. You decide that you want a three scoop cone and that you do not want to repeat flavors. How many possible ice cream cones can you get? (Hint: order matters) [3! = 3 × 2 × 1 = 6]
-
7. Write two of your own questions for this scenario.
Activity 3: Groups
Group students in fours for this activity. [IS.9 - Struggling Learners] Give them the following problem to work on and walk around to answer any questions they may have. Use a big clear bowl with table tennis balls as a visual.
“Let’s say that in your Language Arts class your group of four has to give two presentations. Only two groups present each day. Your teacher uses a lottery system to determine the order of presentations. Each group is assigned a number (1–4). Since you have to give two presentations, the teacher will randomly select a ball and then replace it. So there is a possibility that you may have to give both presentations on one day. Each ball has the same probability. Use this information to answer the following questions.”
-
1. How many outcomes are possible? [16] [IS.10 - All Students]
-
2. Write out all the possibilities that represent this situation. (Note: (1, 1) means the group was chosen to go first for presentation #1 and first for presentation #2.)
-
(1, 1) (2, 2) (3, 3) (4, 4) (1, 2) (1, 3) (1, 4) (2, 1)
-
(2, 3) (2, 4) (3, 1) (3, 2) (3, 4) (4, 1) (4, 2) (4, 3)
-
3. What are the probabilities of each outcome? [1/16 or 0.625]
-
4. What is the probability that group 3 will go first? [1/4 or 0.25]
-
5. What is the probability that group 4 will go at least once on day one?
-
[1/4 + 1/16 + 1/16 + 1/16 + 1/16 = 1/2]
-
What is the probability that one group will go twice on the first day?
-
[1/16 + 1/16 +1/16 = 3/16]
-
Activity 4: Pairs
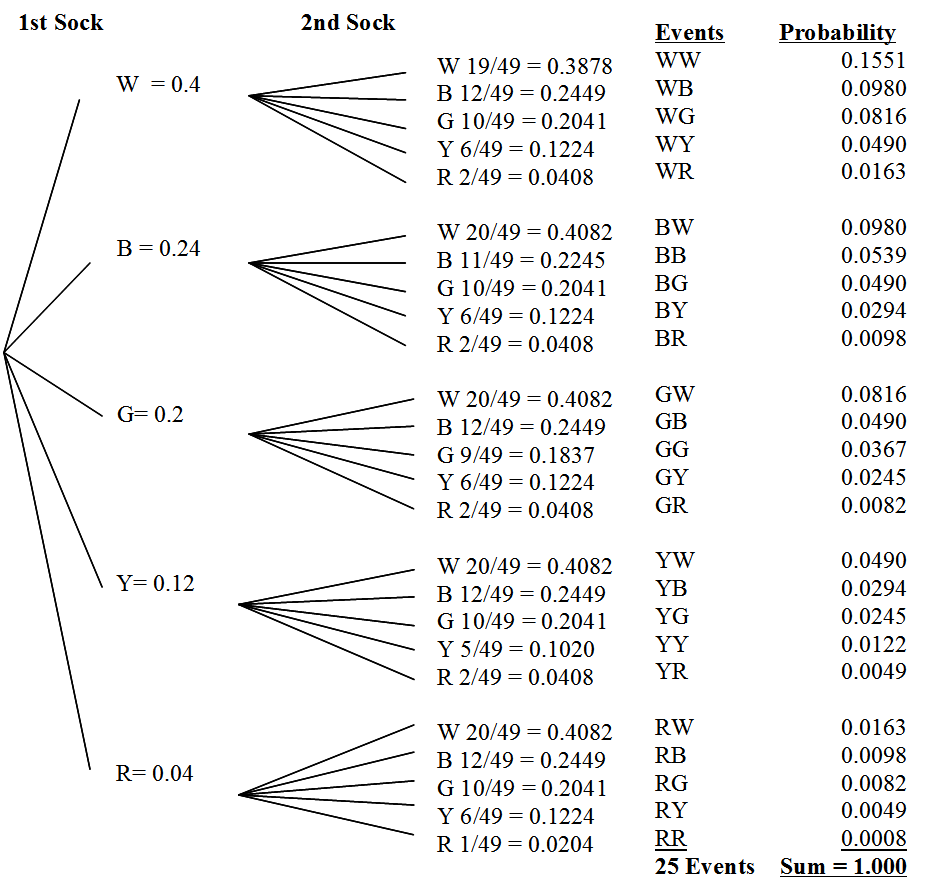
This problem is a tree diagram but involves “without replacement.” Have students pair up and solve the following problem. [IS.11 - Struggling Learners]
You are getting ready for school and your sock drawer is a mess. You have 20 white socks, 12 black, 10 green, 6 yellow, and 2 red.
-
On poster paper, draw a tree diagram for this situation. Be careful to consider what is different about this situation than the other tree diagrams we have drawn. [Hint: once you take a sock out, you do not put it back into the drawer (no replacement).]
-
-
2. What are all the possible outcomes and what is the probability of each outcome?
-
3. What is the probability of picking at least one black sock?
-
[0.0980 + 0.0980+0.0539+0.0490+0.0294+0.0098+0.0490+0.02940.0098 = 0.42634]
-
4. What is the probability of picking one yellow sock or one red sock?
-
(0.48, excludes one yellow and one red)
-
5. What is the probability that both socks are the same color?
- [0.1551 + 0.0539 + 0.0367 + 0.0122 + 0.0008 = 0.2587]
Distribute the Lesson 2 Exit Ticket (M-A2-1-2_Lesson 2 Exit Ticket.doc and M-A2-1-2_Lesson 2 Exit Ticket KEY.doc) to evaluate students’ understanding.
Extension:
Use the following strategies to tailor the lesson to meet the needs of your students throughout the year.
-
Routine: Group and partner work is used throughout so that students can help each other. Emphasis should be placed on communicating mathematical ideas with the specific vocabulary words appropriate to the concepts. The lesson requires accurate note-taking skills to enhance the learning experience while creating a useful resource (notes).
-
Small Groups: Students needing opportunities for additional learning can be placed in one or more small groups to get further assistance from the instructor.
This lesson opens with a problem that is connected to a previous lesson. Probability is an easy topic to connect to real-world scenarios that students can relate to. They like games and they like knowing what their chances are when it comes to certain situations. This lesson has pair work as well as group work because these topics can be difficult for some students and sometimes students explain it best to one another.
