• Lesson 1 Student Document (M-A1-1-1_Lesson 1 Student Document.doc) requires students to articulate their understanding of quadratic equations and standard form, translate trinomials with a quadratic term into standard form, extract information from the graph of a quadratic function, and make multiple representations of quadratic functions.

Show students videos or a slide show of photos (PowerPoint or Photostory would work well) that have visuals of quadratics that can be found in real life. Ask students to think about what these photos have in common as you scroll through them. Give students time to think about the photos and scroll through them again if necessary. Some photos to consider placing in the slide show are the path of a baseball or other projectiles, fountains, a satellite dish, McDonald’s arches, arched doorways in cathedrals, and rainbows. Students should begin to notice they all have a similar shape. Use this idea to introduce the lesson topic on quadratic functions and that the shapes are called parabolas. [IS.3 - All Students]

Display the following notes and examples for students and discuss with them the important vocabulary and properties necessary to understand quadratic equations.

Important Vocabulary:

• Quadratic Equation: An equation with degree (exponent) 2.

• Standard Form: y = ax² + bx + c where a ≠ 0.

• Term: Each part of the quadratic equation separated by a plus or minus sign.

Guide students in arranging the following equations into standard form:

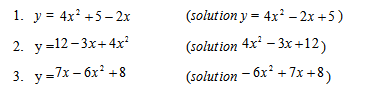
In these problems, students will be reviewing how to move terms of the equations onto one side of the equal sign. This will be important when students get into Lessons 2 and 3. They will also want to practice keeping the “a” term positive; this makes things easier in Lessons 2 and 3. Remind students that a quadratic function is not the same as a quadratic equation. The relationship is a close one, however, because the solution to the quadratic equation is the zero of the corresponding quadratic function.

Have students work independently on the following equations; then discuss the problems with the class: [IS.4 - All Students]

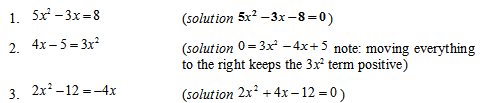
Activity 1: Ordering Quadratics (Kinesthetic, Interpersonal, Synthesis)

Print copies of the Ordering Quadratics Activity sheet (M-A1-1-1_Ordering Quadratics Activity.doc). One set has enough for a class of 30. Add more to the file if your class is larger. Don’t worry if your class does not make perfect sets of three; students will be mixing with one another at their own pace so it will not matter. [IS.5 - Struggling Learners]

Cut out each box/card containing a term and give one to each student.

Hand out to each student the Ordering Quadratics Records Sheet (M-A1-1-1_Ordering Quadratics Records Sheet.doc).

Tell students that they are going to have a time limit to construct as many unique groups of three as they can. These groups must each form a quadratic equation of three terms and record them on their record sheet in standard form. Once they have used the three terms to create one equation, they will need to mix with other classmates to create a new quadratic.

Give students about 1 to 2 minutes to construct as many quadratic equations as possible. Feel free to repeat or adjust the time to meet your classroom needs.

Continue the lesson by displaying the examples of quadratic graphs shown below. Discuss with students the important vocabulary and properties necessary to understand quadratic equations. Guide students to understand that the graph of a quadratic equation has a special shape called a parabola. Note that solution, x-intercept, zero, and root may all be used interchangeably.

The following is a list of characteristics students should be able to recognize and describe on a graph of a quadratic function:

1. Direction of opening (up or down)

2. Location of zeros (where the graph crosses the x-axis; these points represent the solutions to the quadratic equation.) Calculating zeros is discussed more in Lessons 2 and 3.

3. Vertex: The lowest or highest point of the parabola. (Students should be able to locate it and identify its coordinates.)

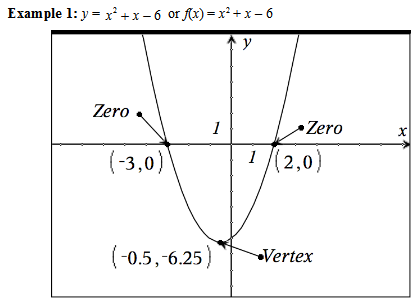
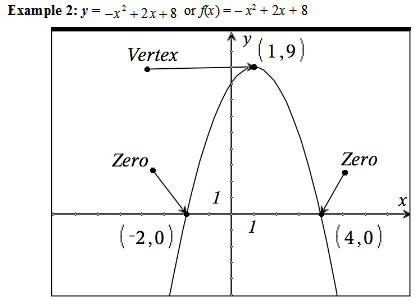
At this time, discuss with students the difference in the openings of each graph. Ask students to think about the differences in the two graphs and the causes, based on their equations. Have students test their hypotheses using a graphing calculator, if available. Give students a few moments to think independently; then ask for a few volunteers to discuss their thoughts. Students should observe that the sign difference on the x² term determines the direction of the opening.

Distribute Graphic Organizer (M-A1-1-1_Graphic Organizer.doc) to show the correspondence between vertex, opening direction, axis of symmetry, and y-intercept. [IS.6 - Struggling Learners]

Use this example to find the vertex of the graph of an equation.

x² + 1 = 0 vertex (0, 1) opens up

Activity 2: Visual, Kinesthetic, Interpersonal Knowledge

Place eight large premade posters of quadratic graphs around the room. Number the graphs from one through eight. When you draw the graphs, it might help students if you place points on the locations of the vertex and zeros so that they can more easily find the coordinate values. Use the following equations when making your graphs.

Divide students into eight groups. Before students move into their groups near the posters, explain the directions:

• Groups will be rotating from poster to poster at your direction.

• When arriving at each poster, the group is to locate and record on a piece of paper each of the following (have the requirements listed on the board so students do not forget what to look for):

1. Coordinates of the vertex

2. Coordinates of the zeros

3. Direction of the opening (up or down)

When groups have examined all eight posters, have students return to their seats to discuss the findings. Go through each poster one by one, discussing the correct answers and answering any questions. You may want to limit questions during the activity to allow students time to really think through the problems and to discuss any difficulties as a whole class so all students benefit. Pay close attention to the tricky problems that involve no zeros and one zero (which is also the vertex); these make great discussion problems.

“Quadratics, like many other functions, can be represented in many different ways. This includes algebraically (equations), tabular (a table of x and y values), graphically, or contextually (such as a real-life scenario or story problem). We will be practicing moving between the different representations.” Show students the following examples of each type of representation.

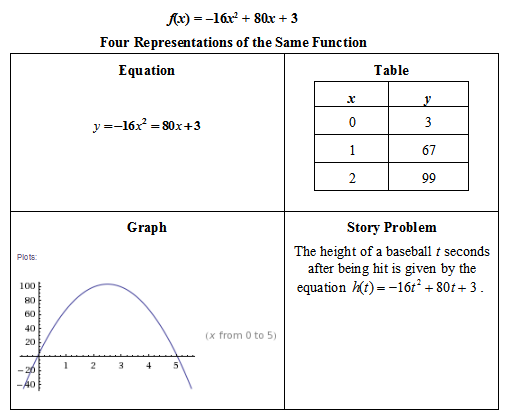
In the Related Resources section there are links to explanations and tutorials on how to use technology to complete the tasks that follow. This is very helpful if you are not already familiar with the statistics, graphing, plotting, and regression generators of the calculators.

Example 1: Given the equation (algebraic representation), find a table, graph, and context:

y = x² + 4x - 5 (given)

Table: (You can use the table function on the graphing calculator to build a table or have students substitute x-values in the equations to build the table manually.) Below is a possible table that can be created from this equation.

Graph: Have students plot the points in their table on a coordinate grid to create the graph. You may have students use the graphing capabilities of the calculator to see the graph as well.

Context: For this step you might want students to try to write their own story problem (synthesis) and discuss their different ideas, or just give students a context to start out with and move to writing their own later in the lesson. Example Context: The length of a rectangle is 4 inches longer than the width, and the area is 5 square inches. Write a quadratic equation that can be used to model the situation. If graphing calculators are not available, skip the example.

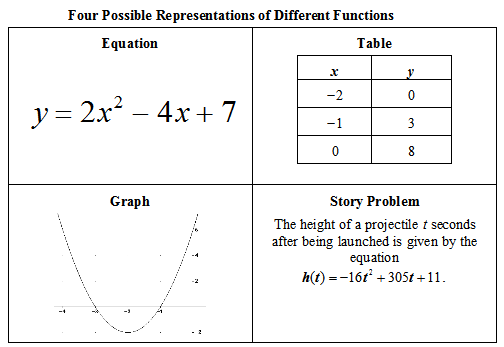
Example 2: Given the table (tabular representation), find the equation, graph, and context.

This task is best done using a graphing calculator (TI-83/TI-84 family). If this kind of calculator is not available, then perhaps students should skip this example or only do the graph and possibly the context.

Table (given):

Equation: y = 2x² - 4x + 3

Graph:

Context: As before, you could have students try to write their own story problem (synthesis) and have a discussion about the different ideas, or just give students a context to start out with and move to writing their own later in the lesson. Example Context: An eagle is diving towards the ground in a parabolic curve. When the eagle is first sighted, it is three feet off the ground. After a second has passed, the eagle is one foot off the ground, but then it pulls away from the ground (still in a parabola). When 3 seconds have passed, the eagle is nine feet off the ground and still soaring. What is the equation that describes the eagle’s motion?

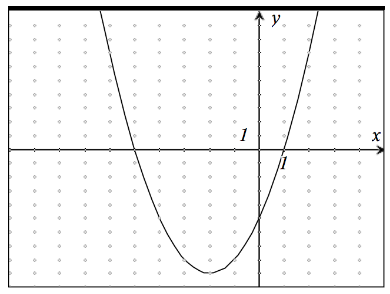
Example 3: Given a graph, find an equation, table, and context.

Graph (given):

Explain to students that, when given a graph, they should find clear points on the graph, place them in the table, and find the equation the same way they did in Example 2. This task is best done using a graphing calculator (TI-83/TI-84 family). If this kind of calculator is not available, then perhaps students should skip this example or only practice making the table.

Table:

Equation:y = -x² + 6x - 4

Context: As before, ask students to suggest possible examples of movement or shapes of objects that look like the parabola. For example, this parabola might describe part of the bow of a naval vessel.

Example 4: Given a contextual situation, find an equation, table, and graph. [IS.7 - All Students]

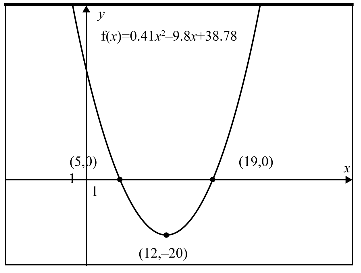
Context (given): Serena is going scuba diving and she begins her dive 5 feet off shore. When diving she goes under water following a parabolic curve. She reaches a depth of 20 feet about 12 feet off the shoreline, and then begins her journey back towards the surface. She reaches the surface of the water approximately 19 feet off the shoreline. Find an equation that models Serena’s path underwater.

Table: Using the surface of the water as the x-axis, we can create coordinates based on Serena’s movements.

Equation: Using techniques discussed in Examples 2 and 3 (quadratic regression), we can generate an equation: f(x) = 0.41x² - 9.80x + 38.78 .

Graph: The graph can be generated both by using the calculator and sketching by hand. The graph shows a scatter plot and the regression equation together.

Activity 3: Small Group Practice

This task is best done using a graphing calculator (TI-83/TI-84 family). If this is not possible in your classroom, refer to the Extension section for an alternate method for this activity. When students are in groups, they should work through each problem individually but use their group members for support. They will want to make sure they know how to do each step in the process, not just parts of it. Encourage students to work together as a group to come up with real-life applications, as this is the most difficult part.

Distribute copies to students of the Quadratic Representations Activity (M-A1-1-1_Quadratic Representations Activity.doc).

This lesson utilizes various learning styles. Use the following suggestions to help tailor the lesson to the needs of your students.

Extension:

• Routine: Distribute the Lesson 1 Student Document (M-A1-1-1_Lesson 1 Student Document.doc) to give students a structured format for taking notes. Provide this resource to students as needed for their success.

• Representations of Quadratics: If there is no access to graphing calculators for students, follow these ideas for ways to modify Activity 3. Students should be able to generate tables and graphs from an equation, table, graph, or story problem without the use of graphing calculator technology. The difficult part will be for them to generate the equation.

  Option 1: If you have access to a few calculators, you can group students so that there is one calculator per group and have students take turns using the calculator.

  Option 2: Eliminate parts of the activity that require the use of a graphing calculator such as using a graph and a table to generate the equation. When working on number 4 in the activity (story problem), you may want to give students the equation if they do not have a calculator to generate it.

  Option 3: If you can project a calculator screen for the entire class, you can lead the class in this activity, with students separated into small groups. Organize the activity so that you can guide students through the calculator portions while they watch, and then instruct students to continue to the other parts of the activity in their groups. This allows you to discuss features as a class and also gives them the opportunity to work on their own.