- [IS.3 - Struggling Learners] Think-Pair-Share: On the board or overhead draw the figures below or a similar setup.
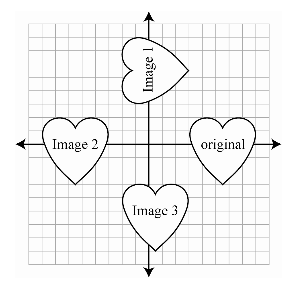
“Consider the figure marked as the original figure. On a sheet of paper take about 2 minutes to write all of the different transformations of the original that you see. Be sure to describe them as specifically as you can, and include the image number in your descriptions.”
Give students 2 minutes to write their observations. Then, ask them to turn to a partner to share their observations (1–2 minutes). Go around the classroom asking each pair to share at least one observation. Be sure to get responses for each of the three images. Observations should include the following:
-
Image 1 is a 90° rotation.
-
Image 2 is a reflection over the y-axis, but it is also a slide motion along the x-axis, 11 spaces to the left.
-
Image 3 has been moved down to the left at a diagonal; it is a combination of sliding down 5 spaces and moving left 5 spaces.
-
“From your observations, I see that you recognized the reflection in Image 2 like we saw in Lesson 1. You also saw the rotation in Image 1, which is what we learned in Lesson 2. You also mentioned a third type of transformation. When we slide a figure right, left, up, down, or a combination of these moves, it is called a translation. The main characteristic of this change is a slide movement.” Point out the slide movements used in the samples on the board.
“In our lesson today we will look at a variety of situations which include translations (slides), and some will also include reflections and rotations.”
Partner Translation Activity
“The slide movement can consist of moving just one direction, like Image 2 in our first example. A figure can be moved horizontally (left or right) or vertically (up or down). What appears to be a diagonal slide is actually two slides, one horizontal and one vertical. Try to identify the translation (slide movements) in the figures your partner creates using pattern blocks.”
Provide each pair of students with a coordinate grid, and a set of pattern blocks or pattern cutouts (M-5-7-2_Coordinate Axes.doc, M-5-7-1_Pattern Cutouts 1.doc, M-5-7-1_Pattern Cutouts 2.doc, and/or M-5-7-2_Pattern Cutouts 3.doc). Have the partners take turns placing one pattern piece on the coordinate grid, along with 2 identical pieces which have been translated with either one or two moves (slides). The opposite partner will try to identify the move(s) in a manner such as “the original figure has been translated left 2 and up 4.” Demonstrate an example on the overhead or on the board to help students understand. Walk around the room observing and assisting where needed. [IS.4 - All Students] Give students 5–10 minutes to continue to alternate turns.
“Now that you are comfortable identifying translations (slides), we are going to work on an activity that incorporates all of our transformations (reflections, rotations, and translations).”
Review the terms translation (slide), reflection (flip), and rotation (turn).
Tetromino Try-outs
“Tetrominoes are 2 dimensional figures made of 4 connected congruent squares. With your partner, you will try to find as many combinations as possible for arranging the four squares. Trace them onto your grid paper as you find them.”
Display the rules for arranging the tiles on the board or overhead projector:
-
Each square must share a common side.
-
Tiles must be laid flat. Stacking is not allowed.
-
Tiles may not be overlapped.
Hand out four 1-inch square tiles and an 8.5 x 11-inch piece of 1-inch grid paper to each student (M-5-7-3_Full Page 1 Inch Grid.doc). If plastic 1-inch squares are not available, the 1-inch tiles can be cut from extra sheets of grid paper.
-
Have students use four squares to try to find as many two-dimensional tetrominoes as possible. Instruct students to trace the combinations onto their two sheets of 1-inch grid paper. When pairs of students believe they have come up with every combination of four squares, they should cut them out to make their own set of tetrominoes.
Discuss the class discoveries, using the following questions to guide students’ thinking:
-
“Do you have all the possible tetromino shapes?”
-
“How do you know?”
-
“Are some of your tetrominoes the same?”
-
“How can you prove it?”(By turning, flipping, or sliding the tetrominoes and placing them on top of each other, we can prove they are the same or different. They are the same when they fit exactly on top of each other, proving that they are the same size and shape.)
There are only five actual tetromino patterns, but students should have come up with several more pieces including many duplicates. At this time do not tell students that they should only have five. Instead, tell students that they will be checking for duplicate congruent shapes caused by rotations, slides, and flips. Demonstrate how they will prove congruence to their partner to start reducing the number of duplicates using phrases to prove congruence such as:
Allow students about 5–8 minutes to narrow down their set to the point where there is no duplication. Check each pair’s final set. The five final tetrominoes shown below are what each student should have remaining. Once each student has the correct set, move on to the Tetrominoes Cover-up Game. Each player should have their own set of tetrominoes for the game.
-
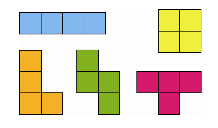
Tetrominoes Cover-Up Game
Students play “Tetrominoes Cover-Up” with the tetrominoes they have just made.
Each pair will need a spinner template and a paperclip to use as the spinner needle when held in place by the tip of a pencil (M-5-7-3_Tetromino Spinner.doc). Students will work at completely covering up the 8 x 6-inch game board grid with their tetromino shapes (M-5-7-3_Game Grid 6 x 8.doc). The object is to have the least number of uncovered squares left at the end of the game without overlapping any tetrominoes. Students may use flips, slides, and turns to place their tetrominoes.
Hand out crayons, colored pencils or markers, a spinner, paper clip, and two game boards to each pair. After the spinner is spun, the arrow will point to a tetromino figure. That figure must be used by the player for that turn. A player whose spin shows “Free Choice” may play a piece of his or her choice. When a piece is used, it should be traced, removed, and its shape colored in on the board. This allows a player to spin the same piece on the spinner and use it on a different turn. Model how to play the game on the overhead projector or board, and explain the additional rules as follows:
-
Each pair will decide who will go first.
-
Player 1 spins the spinner to determine a tetromino piece to play.
-
He/she places the tetromino on the game board so that one side touches either the bottom of the game board or (after the first round) another tetromino.
-
They may use slides, flips, or turns to place the selected tetromino so that the fewest squares will be left uncovered on the game board as the game progresses.
-
The player then traces and colors the squares that are covered by the selected tetromino and places the tetromino back in his/her pile.
-
Player 2 spins the spinner to determine the tetromino to be placed on his/her game board.
-
Play continues until no more tetrominoes can be placed on either game board.
-
The players determine their scores by counting the total number of squares not covered on their own game board.
-
The winner is the player with the lowest score (least number of uncovered squares).
Allow students 8–10 minutes to play the game.
As students are creating their tetromino sets, circulate around the room and ask leading questions to keep students moving toward reducing their sets to the final five. When all students have played the game at least once, discuss with the whole class some strategies they have discovered. The following questions can be used to guide the discussion:
-
“Do certain shapes fit together well?”
-
“How did you decide where to place the tetrominoes?”
-
“Was one tetromino shape more difficult to place than the others? Why?”
-
“What was the easiest tetromino shape to work with? Why?”
-
If time permits, allow students to each play the game again using the strategies discussed. Also encourage students to bring the game home and play it with someone at home.
Have each student complete the Lesson 3 Exit Ticket (M-5-7-3_Lesson 3 Exit Ticket.doc and M-5-7-3_Lesson 3 Exit Ticket KEY.doc). Use the results of this assessment and observations from the lesson activities to determine which, if any, of the suggested instructional strategies below should be used for each student.
Extension:
Use these suggestions to tailor this lesson to meet the needs of your students during the unit and throughout the year.
-
Routine:Discuss the importance of understanding and using the correct vocabulary words to communicate mathematical ideas clearly. During this lesson the following terms should be entered into students’ Vocabulary Journals (M-5-7-1_Vocabulary Journal.doc): tessellation, translation. Keep a supply of Vocabulary Journal pages on hand so students can add pages as needed. Bring up instances of translation and tessellation as seen throughout the school year. Ask students to bring up examples that they see and encourage them to cut out and bring examples to class. They are likely to see these in patterns in a variety of places such as on clothing, household decorations (fabric, wallpaper, floor coverings, posters, pictures, etc.) and on book and magazine covers.
-
Vocabulary:Match Me Up Activity
-
Have students use index cards to create a matching game. Each new word from the unit should be written on a card. Direct students to write a definition, diagram, or example for each vocabulary term on a second card. Each vocabulary word card should have a card to match it. Have students mix up the cards thoroughly and place them face down in a rectangular matrix pattern on the table. On each player’s turn, he/she will draw two cards, with the goal of finding a match of a vocabulary word and its mate (definition, diagram, or example). If students do not pick up a match, they replace the cards. If they find a match, they keep the cards and take another turn. After all the pairs have been matched, the player with the most cards wins. To make the game more challenging for proficient students, each term could have three cards (term, definition, and picture or example). Students would need to find all three cards on one turn in order to keep the trio of cards and continue to look for another matching set on their turn. As with the pairs’ version of the game, cards are returned to their original place and play moves on to the next player if a trio is not found.
-
If computers are available for students, this activity could be used for extra practice. Use this activity for students who could benefit from additional practice with the concepts of rotation and translation, or for any student who needs review. If you have the ability to project to a classroom screen from a single computer, these problems could be used as practice or review for the class or in a class game.
-
-
Practice problems are can be found at: http://www.ixl.com/math/practice/grade-5-reflection-rotation-and-translation
-
Note to teacher: Users are limited to 20 questions per day. Additional problems are only available to members.
-
Use this activity for students who have demonstrated mastery of the concepts in this lesson. Provide each student with a square piece of tag board or part of an index card about 2 x 2 inches, a full sheet of paper or tag board (about 9 x 12 inches), scissors, crayons, and colored pencils or markers.
-
Students will cut a unique pattern from the right side of the square card. Students will either slide the cutout across to the left parallel side, flip it, and slide it across to the left side, or rotate it 90° to the top adjacent side, and then tape it into place.
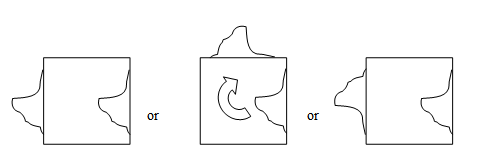
-
-
slide to the left rotate to the top flip then slide left
-
called a translation called a 90° rotation called a glide reflection
-
-
Students can now use this card as their figure to tessellate. The figure that is used over and over again to form a tessellation is called the fundamental region. Students may use their fundamental region and begin tracing it on paper to make a tessellation or they may create a more complex design as their fundamental region. To make a more complex fundamental region, students may start with one of the transformations pictured above, then cut another unique piece from one of the remaining flat sides of the card. They will move that piece to the final flat side by means of a transformation and then tape the piece in place. This more complex figure may then be traced several times on a piece of paper to form a tessellation. A sample of a complex fundamental region using translations is shown below. A piece was cut from the right side and then slid to the left. A different piece was cut from the bottom then slid to the top.
-
-
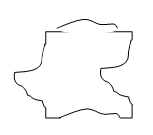
-
If a student is having trouble, you may suggest making a very simple fundamental region. Just make one cutout. Take the cutout design from the bottom corner on the right side, and then slide it to the top corner on the right side. This makes the figure much easier to line up, tape together, and trace.
-
Once the figure is taped in place, students should begin the tessellation by tracing one copy of the design (fundamental region) in the middle of the page. It can be straight or at an angle. They will continue tracing the fundamental region until the page is full. The tessellating piece (fundamental region) will need to be flipped, slid, and/or rotated to fit exactly next to previously placed pieces like a puzzle, without leaving gaps or overlaps on the page. Students can make M.C. Escher-type tessellations that resemble pictures and/or real world objects. Ask students to be creative in designing their fundamental regions to look like a cartoon bird, fish, dog, or tree by adding a few simple details such as eyes, leaves, or feathers and using color. Show the examples below. Many more fun and creative examples can be found online or in books.
-
-

-
This site can be used to demonstrate how to transform a geometric figure and tessellate the resulting figure or to let students experiment with tessellations: http://www.shodor.org/interactivate/activities/Tessellate/
This lesson is exploratory in nature. Students review and compare the characteristics of reflection, translation, and rotation. Students work together to identify translations and use translations to create a set of tetrominoes. Students are asked to use and discuss the use of all three transformations to verify their tetrominoes. The lesson ends with additional activities that allow students to work with combinations of the transformations to create designs observed in the real world.
