1. The Think-Pair-Share activity (Part 2) uses the Graphing Practice Worksheet. Students can evaluate their own and their partners’ understanding of ways to accurately and appropriately represent logarithmic functions graphically. Remind students to apply the principles they already know about functions to make sure their graphs have one and only one y-value for each x. [IS.10 - Struggling Learners]
2. The Lesson 2 Exit Ticket includes a growth/decay model of a real-world application of logarithms and requires student understanding of how to use logarithms as tools to represent a practical problem. Ask students to consider the reasonableness of their answers before completing the work.

This lesson can be fun for students because it illustrates how exponential and logarithmic functions are used in the real world. Ask students whether they like crime shows or solving mysteries. Have a discussion about these shows or mysteries and what students like so much about them.

“Today we are going to learn how exponential and logarithmic equations are used to solve real-world applications. Who can tell me what the most basic exponential equation is and what each part of the equation means?” [IS.4 - Struggling Learners] [y = ab^x or y = ab^x + k; a ≠ 0 (initial value); b is greater than 0 and ≠ 1 (multiplier: describes a percentage increase or decrease); and k = asymptote (a value that the function gets close to but never touches)]

Part 1

Exponential and logarithmic functions are used in the real world. Most notably, exponential functions are used in population growth, interest, and bacterial growth. Logarithmic functions are used to measure light and sound intensity, as well as measuring magnitudes of earthquakes. Review how to convert back and forth from exponential form to logarithmic form since students will be doing this when graphing logarithmic equations.

“Today we are going to learn how to graph exponential and logarithmic functions without the use of a calculator. We will begin with the equation, make a table of values with a few points, and sketch the graph.”

“Suppose we have the exponential function, y=3x; we can use a table of values to graph the function.”

“Let’s fill in our table.” Using a projector or interactive whiteboard, display the following chart: [IS.5 - Struggling Learners]

“Now, we can create our graph.” Display the following graph:

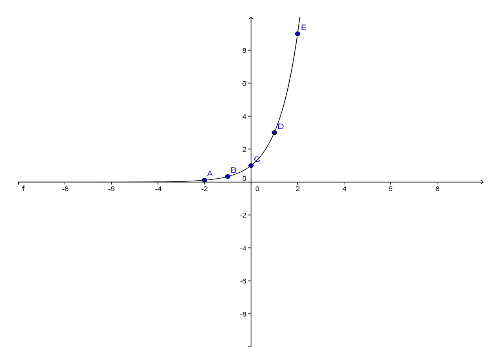
“Notice that the graph approaches a horizontal asymptote of y = 0”

“Now, let’s graph a logarithmic function!”

“Since a logarithmic function is the inverse of an exponential function, we simply graph the exponential function that is the inverse, draw the line of symmetry, y = x, and plot the reverse coordinates for each point on the exponential function. An illustration will make this process easier to understand.”

“Let’s take our exponential function from before, y=3x. The inverse of this function is log3x.”

“Let’s look at our table from before and insert another column for the ordered pair containing the reversed coordinates.” [IS.6 - Struggling Learners]

“We will now graph the points for the logarithmic function.” Display the following graph:

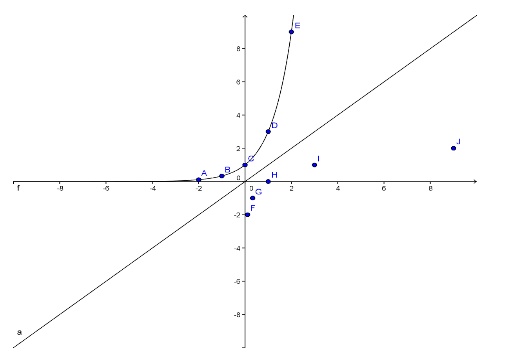
“Now we simply have to connect the points of the logarithmic function. Note the vertical asymptote of x = 0.”

Part 2

“Before we can get to the application problems, we have to learn about a few formulas. Let’s say we have to solve 5x = 50. What do we do to solve for x?” (divide both sides by 5) “Division is the inverse of multiplication. So what is the inverse of exponents?” (logarithms)

“If we have a problem like 2^{x – 1} = 8, we can simply rewrite 8 as 2³ and then set the exponents equal to each other and solve for x.”

2^x−1 = 8

2^x−1 = 2³

x−1 = 3

x = 4

“But what if we don’t have the same bases to work with? We can take the logarithm of each side of the equation.” Put the following formulas on the board and do the examples as a whole class.

log b^x = log a
x logb =log a
or

“Remember that ln refers to the natural logarithm, not the base 10 logarithm. It’s important to keep in mind that these are two different bases. The base of the natural logarithm is approximately 2.71828 and is quite useful in many fields of mathematics.”

“When we write log without a base next to it, it is the Common Log, base 10.” [IS.7 - Struggling Learners]

“Let’s try some examples.” Examples should be worked out together as a class. Note that there are multiple ways to solve these equations.

1. 2^x = 10

Answer for number 1:

x=log10log2

2. 2^x = 10

Work for number 2:

log2x=log10

xlog2=log10

x=log10log2

3. 5^x = 45

Work for number 3:

log5x=log45

xlog5=log45

x=log45log5

4. 8^x-1 = 100

Work for number 4:

log8x - 1=log100

(x-1)log8=log100

x-1=log100log8

x=log100log8 + 1

5. 6^{2x + 3} = 50

Work for number 5:

log62x+3=log50

2x+3log6=log50

2x+3=log50log6

2x=log50log6-3

x=log50log6-32

“Let’s look at a natural logarithm example. Suppose we have the exponential equation: 4e3x + 5 = 10. We can use the natural logarithm to solve the equation, since we have e as a base. The base of the natural logarithm, e, operates in the same way as base 10. A logarithm is the inverse of an exponential function. Log (1000) = 3 because 10³ = 1000. In the same way, e³ ≈ 20.08553, so ln (20.08553) ≈ 3.” Work through with students: [IS.8 - Struggling Learners]

4e3x+5 = 10

4e3x=5

e3x=1.25

lne3x = ln1.25

3x=ln1.25

x=ln1.253

x≈.07

“If we are given a logarithm and asked to evaluate, we can use the change of base formula. We can also convert the logarithm to another base.”

“Let’s explore how to evaluate a logarithm in terms of common logarithms using the change of base formula first .” (Review this concept as a class.)

logbM=logcMlogcb

*For all positive numbers b, c, and M, where b ≠ 1 and c ≠ 1.

“For example, take this logarithm.”

log214 = log14log2

≈3.81

“Now, we can also convert this logarithm to another base. Let’s convert it to base 6.” Work through with students:

log214=log6x

3.81≈log6x

x≈63.81

x≈922.05

“Now we are going to get into some fun problems. We will do an example as a class, then you will solve a few problems in groups.”

Give the following problem.

Aunt Helen likes drinking tea, but she is specific about the temperature at which she drinks it. She boiled the water (100^o C) and poured it over the tea leaves. Five minutes later she came back and the tea was 65^o. Aunt Helen keeps her house at a cool 20^o. Write an equation that represents the temperature of Aunt Helen’s tea.

“First we need to determine what we know. We know that at time t = 0 (the time at which the water has come to a boil), y (the temperature of the tea) is 100 and that when t = 5 (the number of minutes it has been left to sit after it came to a boil), y is 65. What else do we know from the problem?” (Room temperature is 20^o, which is the asymptote, since nothing will cool down more than room temp.) “We will substitute the first point into an exponential equation and first solve for a. Then we will substitute the second point and solve for b. This will tell us the percentage rate at which the tea cools per minute.” Work through with students:

100 = ab⁰ + 20
80 = a(1)
a = 80

65 = 80b⁵ + 20
45 = 80b⁵
0.5625 = b⁵
b ≈ 0.8913

y = 80(.8913)^t + 20

“We can use this equation to make predictions. Let’s say Aunt Helen only likes to drink her tea when it is 50^o. How long will she have to wait to drink her tea?”

50 = 80(0.8913)^t + 20
30 = 80(0.8913)^t
0.375 = 0.8913^t

“Now we have to use the change of base formula to solve for t.”

t = log 0.375 ÷ log 0.8913 or ln 0.375 ÷ ln 0.8913 ≈ 8.5 minutes [IS.9 - Struggling Learners]

Activity 1

Hand out the Solving Exponential and Logarithmic Applications Worksheet (M-A2-4-2_Solving Exponential and Logarithmic Applications Worksheet.docx). Students should work on this worksheet in groups since solving application problems can be difficult for some. Go over the worksheet when everyone is done. Note: students may want to wait to answer the graph question until after participation in both parts of the lesson.

Activity 2

Hand out the Graphing Exponential and Logarithmic Functions Notes (M-A2-4-2_Graphing Exponential and Logarithmic Function Notes and KEY.docx). Go through the notes with students as well as the practice problems.

Activity 3

Hand out the Graphing Practice Worksheet (M-A2-4-2_Graphing Practice Worksheet.docx). Have students begin this worksheet on their own. After a little bit, they can pair up with a partner to check work. When everyone is done, have students bring their answers and work to the board.

Activity 4

Hand out the Lesson 2 Exit Ticket (M-A2-4-2_ Lesson 2 Exit Ticket.docx) to evaluate whether students understand the concepts.

Extension:

1. Using the Graphing Practice Worksheet, discuss what would happen to the graphs if the parameters were changed to another number. For example, ask students the following questions:
2. “What if k were −5 in #1? What would we have to do to our current graph?” (move the graph down eight units)
3. “What if h were 3 in #2? What would we have to do to our current graph?” (move the graph to the right four units)
4. Have students write their own equations and have a partner graph them.