1. The Lesson 3 Exit Ticket activity uses two real-world growth/decay models of logarithmic growth to evaluate student understanding of increases and decreases of quantities over time. Students’ understanding of the correspondence between each component of logarithms to the specific characteristics of the models will indicate their level of understanding. [IS.7 - Struggling Learners]

Have a discussion about the students’ future. “Why do you want to go to college? What are your career interests and what kind of career do you want? Who would like to travel or have a family? Why do you want to do or have any of these things for which saving and accumulating some money is a useful goal?” (discussion)

“These are all events for which saving money can be an intelligent decision. Saving money is a good example of exponential growth. Consider this example. If one were to save one penny on day one, then double that amount every day for 30 days, how much would one accumulate by the end of the month?” (approximately $5.36 million)

Part 1

“Before we can get into writing more equations like this, we have to discuss percentages and multipliers. [IS.6 - Struggling Learners] Does anyone know why in our example we multiplied by 1.1 when we increased our savings by 10%?” (It’s okay if no one knows; that’s what the beginning of this lesson is about.)

(The following problem can be done as a whole class. After this example students will do some problems on their own.)

Display two grids of equal size.

“Let’s say we are going to buy something that costs $100.” Point to the grid on the left and explain that this grid represents the whole cost.

“We found a coupon for 15% off. Let’s shade in the discount in the grid on the right and see how much the cost is after the discount.”

“Algebraically, how could we solve for the discount?” (Tailor the conversation around students’ prior knowledge of percents. They should remember that when we use percents in calculations, we have to change them to decimals.)

“Our item costs $100, but we have a 15% discount. So we multiply 100 by 0.15 to get the discount. From here we subtract the discount to determine our final cost; which is what?” ($85)

“How could we do this if there were a percentage increase, like a tax or a tip?” (Encourage discussion and find out what students know about percentage increases. Below are some questions to use if students are not volunteering their thoughts.)

• “Using the same grid I have, what if there was a 6% tax on my item instead of a discount? How much am I going to pay?” ($106)

• “How many squares am I going to fill in?” (6)

• “Do we subtract those squares to determine my final cost?” (no)

The discussion should be how you pay 100% plus an additional 6%, meaning you add not subtract.

Hand out the Percent Grids Worksheet (M-A2-4-3_Percent Grids Worksheet and KEY.docx). “With a partner, you will be determining costs after different situations, such as discounts, taxes, and tips. After you and your partner have finished, get together with another pair and check your work. Be careful on the sheet. Not every grid has 100 squares!”

When students are done with the grids, leave them in their groups of four. Challenge them to see whether they can come up with a formula or an equation for a percentage decrease and a percentage increase. After some time, bring the class back together to discuss multipliers.

“Let’s go back to my first example, but let’s say we do not know the price. We’ll call it X. To find the discount, we changed the percent to a decimal, then multiplied it by the original price. Then what did we do to find the final price we paid?” (subtracted)

“Let’s look at the algebraic expression.” Write on the board:

Original Price – Discount = Final Price

X – (.15)X = .85X

“Let’s think about this. If we get a 15% discount, what percent is left over?” (85%) “So the shortcut to finding out how much something costs with a discount is to just multiply the price by the percentage (as a decimal) left after the discount. Let’s look at our tax example.” Write on the board:

Original Price + Tax = Final Price

X + (.06)X = 1.06X

“When we have a percentage increase, we are paying for 100% of the item plus the increase. So we have 106% left over, which is 1.06 as a decimal. This means the shortcut to finding out how much something costs with an increase is to just multiply the price by 1 plus the percent increase (as a decimal). Let’s do a few examples.”

Find the multipliers for the following situations as a class:

“In this lesson, we are going to learn about functions that do not grow or decline by a constant rate but by a constant percentage. Let’s take a look at an example. Let’s say we have $5 and we save 50¢ a month. How much money would we have after a year? Make a table of values to determine this and write an equation.” Lead students through the process of creating the table.

Equation: y = .50x + 5

“Now let’s say that we save 10% of our money each month. How much is 10% of $5?” (Allow students time to answer.) “Right, $0.50. So after one month we would have $5.50. Now the next month, we save 10% of $5.50. Which is how much? Let’s make a table of values to determine how much money we would have after one year and write an equation. Then we will compare saving 50¢ versus 10%.” (For this part of the lesson you will have to guide students on how to write the equation, but wait to go into details until later on in the lesson.)

Equation: y = 5(1.1)^x

“In our first example our values increased by .50. Is that the case here? Since we do not go up by the same value but by the same percentage, we have to divide to find out what we MULTIPLIED by each time. 5.50/5 = 1.1. What do we use to summarize repeat multiplication?” (exponents)

“So we started with $5 and kept multiplying by 1.1; so our equation would be what?”

“Let’s use our table of values to create a graph of the exponential growth function.”

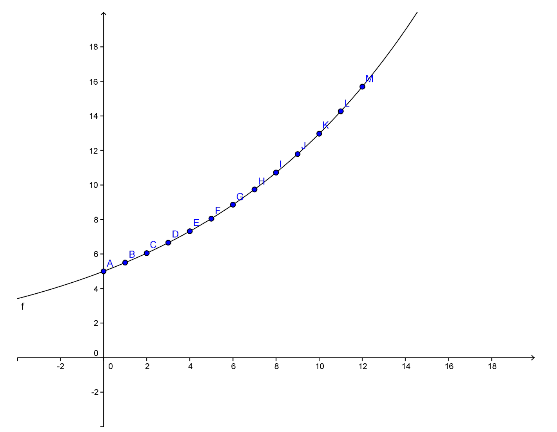
“We just looked at an exponential growth function. An exponential growth function can be written in the form, y = ab^x, where b > 1. An exponential decay function can be written in the form, y = ab^x, where 0 < b < 1.”

“Here are a couple of examples, y = .6(3)^x and y = 10(.41)^x. These examples represent exponential growth and exponential decay, respectively.”

Remind students to reread the definitions of exponential growth and exponential decay in the vocabulary section.

Part 2

“Now that we’ve learned how to write the multipliers of percentage changes, let’s take a look back at our introductory example. We started with $5 and we were saving 10% each month. What was our multiplier?” (1.10) “We started with $5. To find out how much we have after one month, we multiply by 1.1 to get $5.50. To find out how much we have after two months we multiply 5.50 by 1.1. Our equation would be y = 5(1.1)(1.1)(1.1)…=5(1.1)^x. The initial value, or starting amount is 5, and 1.1 is the multiplier. This is called exponential growth.”

Hand out copies of the Exponential Growth and Decay Notes (M-A2-4-3_Exponential Growth_Decay Notes and KEY.docx) and fill in as a class.

Have the following problems written on the board. Students can write their answers on the back of their note sheet.

“Write an exponential equation for the following situations.”

1. a car valued at $5,340 that depreciates 14% per year                    [y = 5340(.86)^x]

2. an antique painting valued at $200 appreciates 9% a year           [y = 200(1.09)^x]

3. a bank account with $20.45 earns 4.5% interest a year                [y = 20.45(1.045)^x]

4. 100 grams of a radioactive isotope decreases 45% a year           [y = 100(.55)^x]

“Notice that the numbers that represent b are less than 1 but greater than 0 in the exponential decay cases. Also, notice that b is greater than 1 in the exponential growth cases.”

Part 3

“What if we weren’t given the initial value or percentage rate and we needed to write the exponential equation? For example, let’s say my savings account earns 5% interest a year and after 2 years I had $325 in my account. How much money did I start out with?” (Write this information on the board and give students some time to think about it. One or two students may come up with it.) “What are we solving for?” (initial value)

Ask whether any students would want to show their ideas or work on the board.

“We know our multiplier is 1.05. Since x represents time, I am going to substitute 2 for x. Where should I substitute 325?” Discuss the equation with students:

325 = a(1.05)²          325 = a(1.1025)          a = 325 ÷ 1.1025 ≈ $294.78

“What if I knew I invested $300 initially and that after 3 years I had $358? What are we solving for now?” (multiplier)

Ask students how they would go about solving for the multiplier. Go through the process together.

358 = 300(b)³ 1.19 = b³ Cube root both sides or raise both sides to the 13 power

b ≈ 1.06

Hand out the Exponential Growth and Decay Worksheet (M-A2-4-3_Exponential Growth_Decay Worksheet.docx). Students can work on this in pairs. Walk around and check their work, ask questions. See how they do when they get to the last three questions. If the class is stuck, then bring the class back together.

“What if we have two points on the graph and neither one of them is the initial value? For example, let’s say in a science experiment we counted 220 bacteria after 2 days and 275 bacteria after 4 days. How many bacteria were there initially and at what rate are they growing?” (See whether students have an idea of how to begin the problem.)

“Let’s put the two points into a table.” Write on the board:

“Since we multiply in exponential equations, we divide 275 by 220. We get 1.25. How many times did we apply the multiplier to get from 2 days to 4 days?” (twice)

“Since we multiplied a number twice, we have to take the square root of 1.25 to get our multiplier. Our multiplier is approximately 1.118, which means the bacteria are growing by what percent each day?” (11.8%)

“Now how do we find the initial value?” (substitute the multiplier into the equation with one of the given points)

Give students time to finish the worksheet knowing what they know now.

Final Activity

Hand out the Lesson 3 Exit Ticket (M-A2-4-3_Lesson 3 Exit Ticket and KEY.docx) to evaluate whether students understand the concepts.

Extension:

1. Students need a graphing calculator for this activity. Hand out the Population Estimates spreadsheet and the Stat Plot Instructions (M-A2-4-3_Population Estimates.xlsx and M-A2-4-3_Stat Plot Instructions.docx).
2. They can either pick the national data or pick a state of their choice (D.C. has good data). Because the numbers are so large, the data appears more linear, but discuss with the class what type of function would make more sense. Does a population generally increase by the same number each year or the same percentage?
3. Have them answer the following questions: What is the multiplier, and what does it represent in terms of the population growth? What is the initial value, and what does it represent? How many years will it take for the population to double?