·         Student responses during modeling are useful indications of skill in manipulating terms, but specific kinds of errors can reveal more fundamental misunderstanding. For example, note instances where students indicate division but fail to use reciprocal multiplication. [IS.10 - All Students]

·         Performance during the partner activity will be productive to the degree that partners listen to each other, self correct, and explain their reasoning. [IS.11 - All Students]

·         Responses on the independent practice worksheet are useful when error analyses reveal specific types of misunderstanding that are shared by multiple students.

“We have had much experience solving equations of the form 2z + 12 = –5x – 9  andx² + 5x + 6 = 0, but today we will be looking at equations that involve fractions with variables in the denominator. This lesson will focus on the process involved during solving equations involving rational expressions. The key to this lesson is to take a more complex type of equation and turn it into an equation that we already know how to solve, like 2x + 12 = –5x – 9 and x² + 5x + 6 = 0.” [IS.4- All Students]

“For example, the following is a rational equation: 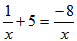 because it has x in the denominator. To solve this problem, as well as other rational equations, follow these handy steps.”

Display each step for students to record in their notes and refer back to these steps as you go through each example below. [IS.5 - Struggling Learners]

1.

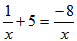
Step 1: Make sure all denominators are in factored form: [IS.6 - All Students]

“What is the denominator of the first fraction?” (x)

“Can this be factored any further?” (no)

“What is the denominator of the second fraction?” Students should note that 5 is the same as 5 divided by 1.

“Can this be factored any further?” (no)

“What is the denominator of the third fraction?” (x)

Step 2: Multiply the entire equation by the factors of the denominators (least common denominator):

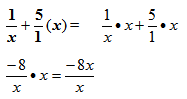
Step 3: Divide by a common factor within each term where necessary and record what remains: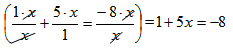 

Step 4: Use basic algebra techniques to solve the remaining problem. (Note to students that what they will be left with is a type of equation that they have been able to solve for some time now.)

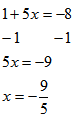
Step 5: Check for extraneous solutions. By substituting the solution for the variable, check that solution(s) are defined for the original problem. Explain to students about the possibility that solutions might be generated that are not permitted in the original problem because they create an undefined value. These values are not part of the domain and should not be included in their final answer. We want to avoid getting 0 in the denominator, so we must check to make sure that it does not happen with our calculated values.

(– 9/5) would not create a zero denominator and thus ( – 9/5 )is the solution to this problem.

Guide students through the remaining examples. Make certain to emphasize each of the five steps as you go. The problems get more difficult as you go.

[IS.7 - All Students]

[IS.8 - Struggling Learners]

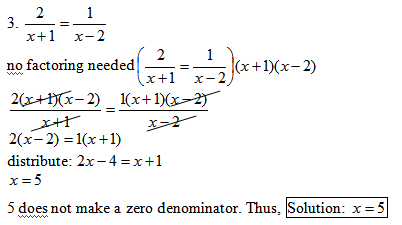
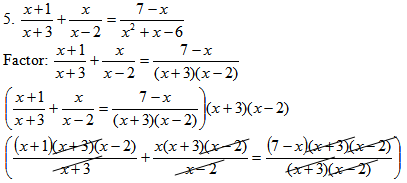
(x + 1)(x + 2) + x(x + 3) = 7 - x
FOIL & distribute: x² – x – 2 + x² + 3x = 7 – x
combine like terms: 2x² + 2x – 2 = 7 – x
Since there is a squared variable, it is most likely that factoring will be necessary to solve the problem. Be sure to discuss with students that when they see a squared variable that they should recognize factoring will most likely be the required method for solving the problem.

Thus, 2x² + 3x – 9 = 0

(x + 3)(2x – 3) = 0

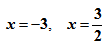
When checking solutions we find that −3 makes a zero denominator, but (3/2) does not. Thus, Solution:  x = (3/2)

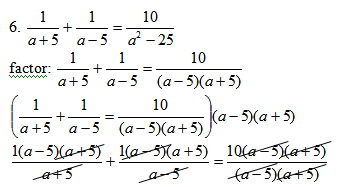
a – 5 + a + 5 = 10

2a = 10

a = 5

a = 5 would create a zero denominator and thus cannot be a solution to the problem, leaving us with no viable solutions. Thus, Solution: NO SOLUTION Ø

[IS.9 - All Students]

Review:

·         Interpersonal Partner Activity: After modeling examples and procedures to students, allow them to get some practice using the following activity. During the activity you should have students work with a partner so they can help guide each other and discuss their way through each step.

·         Display the M-A2-5-2_Solving Rationals Partner Activity.ppt problems for students, one at a time. Once displayed, students should work with their partner to solve the problem as modeled in class. Hand-held white boards can work well here. Give students an appropriate amount of time, walk around to help students, and address problems where necessary. You may want to display answers or work out the solutions on the board to help students realize any mistakes. Repeat the same process with each problem in the PowerPoint.

·         Independent Practice (Jokes Worksheet): This worksheet is designed for students to get some independent practice with the problems they have been working with in class, while adding a fun little joke into the mix. Students will have seven problems to solve in which each solution will correspond to a letter. Correctly solving each problem will spell out the answer to a fun riddle. (M-A2-5-2_IP Jokes WKS.doc) Solution: NICE BELT.

Extension:

·         Use guided notes sheet provided in resource folder for students who need opportunity for additional learning (M-A2-5-2_Solving Rationals Guided Notes.doc).

·         Applied Problem: Car A travels 180 miles in the same time it takes Car B to travel 120 miles. If one car is going 20 mph faster than the other car, find the speed of both cars.

Solution: One car 40 mph, the other car 60 mph.
                       

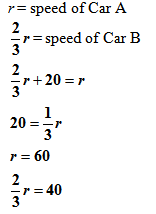
·         Modification 1: Students with special needs. If possible, print the problems ahead of time and have students work on them according to their appropriate needs.

·         Modification 2: Possibly have those students who are at or going beyond the standards work with other students who need opportunity for additional learning so the teacher can reach more students.

·         Modification 3: If there is not enough class time available, print off the problems and give them to students as an independent homework assignment.

·         Modification 4: Do everything individually. No partners.