Simplifying Complex Rational Expressions

Objectives

In this lesson, students will simplify complex fractions. Students will:

· apply concepts from simplification of rational expressions to those written in complex form.

· apply multiple simplification techniques to their simplification process.

Essential Questions

· How can we extend arithmetic properties and processes to algebraic expressions and processes and how can we use these properties and processes to solve problems?

Vocabulary

· Expression: A variable, or any combination of numbers, variables, and symbols that represent a mathematical relationship (e.g., 24 × 2 + 5 or 4a – 9). [IS.1 - Preparation]

· Rational expression: An expression that is the ratio, or quotient, of two polynomials.

Duration

180–270 minutes [IS.2 - All Students]

Prerequisite Skills

Prerequisite Skills haven't been entered into the lesson plan.

Materials

· copies of Complex Guided Notes (M-A2-5-3_Complex Guided Notes.doc) [IS.3 - Struggling Learners]

· copies of Complex Fractions Group Activity (M-A2-5-3_Complex Fractions Group Activity and KEY.doc)

· copies of Complex Fractions Extra Practice (M-A2-5-3_Complex Fractions Extra Practice and KEY.doc)

Related Unit and Lesson Plans

Related Materials & Resources

The possible inclusion of commercial websites below is not an implied endorsement of their products, which are not free, and are not required for this lesson plan.

https://www.youtube.com/watch?v=01UAMu531og video showing process of simplifying multiple types of complex fractions, from basic to more complicated
https://www.youtube.com/watch?v=q4aMMtSvsvI&feature=related video shows a slightly different method of solving a complex fraction involving addition in the numerator (LCD-Multiply-Divide Method)

Formative Assessment

View

· Extension activity allows for differentiated assessments according to individual student needs. Students can self assess while working in groups. [IS.10 - Struggling Learners]

· Performance on extra practice worksheet will give partial indication of level of individual student understanding. Note the types of errors and skipped exercises.

Suggested Instructional Supports

View

Active Engagement, Modeling, Explicit Instruction

[IS.9 - All Students]

W:	This lesson flows logically from lesson one, where students learned how to perform operations on rational expressions. This lesson will take these concepts to the next level by combining them in different ways. Students should understand how these concepts relate to one another and that they will be expected to perform these tasks efficiently.
H:	The beginning of this lesson will provide students an opportunity to recall many of the important skills necessary to complete the lesson. This will show students that they already have much of the knowledge necessary to work through these problems. This will help students gain the confidence necessary to make it through these long problems, as well as make the connection between their prior knowledge and where they are headed.
E:	During the lesson, three students will be provided with modeled examples to equip them with the skills necessary to complete these problems. Students will have a chance to work through problems and receive feedback on their work so they are prepared for independent tasks.
R:	The structure of this lesson allows students time to reflect and revisit these concepts after each sub-topic is presented. Thus, students can determine whether they have any questions prior to learning the next scenario. If needed, the teacher can provide students with alternate explanations or more time to revise their work.
E:	During this lesson students will have the opportunity to express their understanding through the use of a group activity and independent practice. The independent practice problems are designed to give students a chance to try some problems on their own after the teacher discusses the procedures of the problems with them. This way, students may evaluate their work and determine whether they still have questions. The group activity allows students to gain a deeper understanding by working cooperatively with other groups. This way they can teach and learn with one another.
T:	The extension portion of this lesson provides the teacher with many meaningful activities and options to help meet the needs of a diverse learning community. The guided notes, group activities, and independent practices provided are designed to tailor this lesson to your classroom needs.
O:	The organization of this lesson follows a pattern that begins with teacher modeling of one type of problem, and then students have the chance to try a few on their own. This repeats for each of the three types of problems discussed in the lesson. After the lesson is complete, students will then work together on a group activity. This provides them with time to reflect and build up their skills necessary for these problems.

IS.1 - Preparation

Consider using graphic organizers (e.g., Frayer Model, Verbal Visual Word Association, Concept Circles) to introduce and review key vocabulary prior to the lesson. Other key vocabulary to consider would be complex fractions, numerator, denominator, reciprocal, ratio, quotient, polynomials, simplify

IS.2 - All Students

Consider preteaching the concepts critical to this lesson, including the use of hands-on materials. Throughout the lesson (based upon the results of formative assessment), consider the pacing to be flexible to the needs of the students. Also consider the need for reteaching and/or review both during and after the lesson as necessary.

IS.3 - Struggling Learners

Consider providing struggling students with time to preview/review information on simplifying complex rational expressions at www.khanacademy.org .

IS.4 - All Students

Consider using a visual approach such as a number line and examples of operations with fractions to aid struggling students in their recall of the procedures. See http://www.visualfractions.com/ for a visual fraction tutorial that can be used by students, teachers and parents in their quest to develop conceptual understanding of fractions and aid in the transfer of this knowledge to working with operations on complex numbers.

IS.5 - Struggling Learners

Consider providing struggling students with a copy of the problems including completely worked out solutions for the first couple of problems of each operation (adding, subtracting, multiplying and dividing with complex numbers). Gradually cut back on the completeness of the solutions and leave space for the students to complete missing steps on their own.

IS.6 - Struggling Learners

It may be beneficial to complete this activity in groups (small or large) so that struggling learners may communicate with others and benefit from the thinking processes that are shared. Be sure that conversations are facilitated within the group(s) so that student thinking is shared.

IS.7 - Struggling Learners

Consider providing struggling students with a copy of the problem so that focus can be on solving the problem, not copying it from the board.

IS.8 - All Students

Consider facilitating a discussion consisting of advancing / assessing questions and student/teacher Think Alouds that help struggling students make connections as they deepen their understanding of working with complex numbers. Consider viewing the publication, Teachers’Desk Reference: Essential Practices for Effective Mathematics Instruction in order to review the sections on formative assessment as well as assessing and advancing questions. This publication can be found at: http://www.pattan.net/category/Resources/PaTTAN%20Publications/Browse/Single/?id=4e1f51d3150ba09c384e0000

IS.9 - All Students

Also consider Think-Pair-Share, Random Reporter, Think Alouds, Math Journal, and use of graphic organizers. Information on Think-Pair-Share and Random Reporter can be found on the SAS website at, https://www.pdesas.org/Main/Instruction

IS.10 - Struggling Learners

Prior to teaching this lesson, consider the prior knowledge of struggling students as well as misconceptions that are likely to surface. Have a game plan for how to correct misconceptions and connect current concepts to prior knowledge.

Instructional Procedures

View

This lesson is composed of four parts. Part one involves a concept recall activity. Parts two and three involve modeling three different types of complex fractions students may encounter. As you go through each example with students, make sure to emphasize the techniques that were used in lesson 1. Students should understand that they are doing the same procedures, just combined in different ways.

Part 1 Concept Recall

Display or state the following statements to the class. [IS.4 - All Students] These are designed to allow students some time to recall some of the important concepts of simplification of rational expressions and solving of rational equations that will be important for this lesson.

1.      When adding or subtracting fractions we must have a __________________. (common denominator)

2.      When multiplying fractions we can __________ if we see there is the same factor on the top and bottom. (divide by a common factor)

3.      When dividing fractions we must __________ & ____________ the second/bottom fraction. (multiply by reciprocal)

4.      Don’t forget to always make sure your expressions are in ____________ form. (factored)

Part 2 Basic Complex Fractions [IS.5 - Struggling Learners]

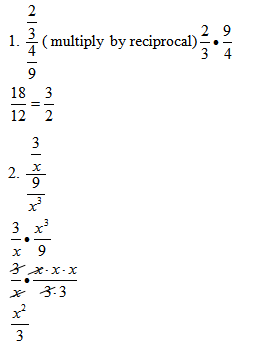
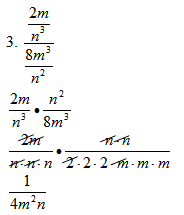
Part 3 Complex Fractions that involve factoring

1.

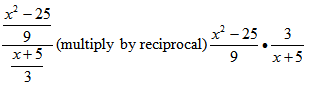
Note. This problem now becomes a problem identical to what was done during lesson 1.

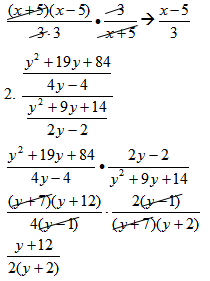
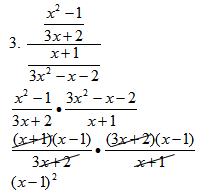
Part 4 Complex Fractions involving addition and subtraction [IS.6 - Struggling Learners]

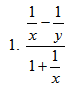        Remind students at this point to work at getting common denominators. It may also be helpful for students to work through the top expression and bottom expressions separately and then combine them together last.


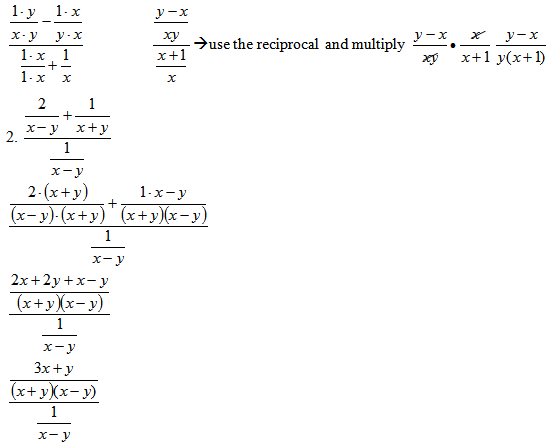
Now that the fractions have been simplified enough we can now use the reciprocal and multiply step

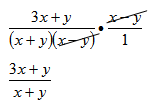
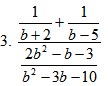
Instructor Note: When approaching this problem with students it may be a good idea to address the numerator expression first, then simplify the denominator expression, and then in the final step put them together with the reciprocal and multiply step. This may eliminate confusion for students trying to address too much at once.

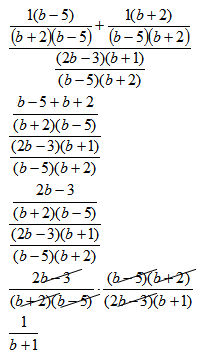
Review:

·         Group Activity: Use the group activity to allow students to practice applying the concepts from the lesson as well as providing them with an opportunity to work together (M-A2-5-3_Complex Fractions Group Activity and KEY.doc).

o   Groups must consist of three students.

o   The activity contains three problems. Give the groups the problems one at a time by writing each problem on the board. [IS.7 - Struggling Learners]

o   When working with the problems the group members’ goal is to work together to solve the problem. Therefore, each member of the group will be assigned a role for each problem. After problem one, the roles will switch so that each student will have an opportunity to perform each role. Role 1: simplifies the numerator expressions, Role 2: simplifies the denominator expressions, Role 3: performs the reciprocal and multiply step to simplify the two expressions together.

o   After all groups are finished with the problem, discuss the solution with the class, have students switch roles and display the next problem on the board, then repeat the process.

·         Use guided notes sheet provided in the resource folder for students who need opportunity for additional learning (M-A2-5-3_Complex Guided Notes.doc).

·         Alternate to Group activity.

·         Print out a copy of the three problems used in the group activity and assign them for homework.

·         Have special needs students work in groups guided by a special education teacher/aide.

·         After each subgroup of examples, provide students with problems to attempt on their own, either as homework or in class. [IS.8 - All Students] This will give students time to reflect on the concepts discussed and the teacher time to see where any problems are occurring (M-A2-5-3_Complex Fractions Extra Practice and KEY.doc).

·         Switch the order of presentation of solving of rational equations and simplification of complex rational expressions. Some may find this more beneficial because many of the concepts used in this lesson are taught throughout the process of simplification of rational expressions. Therefore, these concepts would be fresher in students’ minds and may allow them to work through the problems in lesson 3 more easily.

Extension:

·         A family made a driving trip over two days. On the first day they traveled 75% of the distance at 75 miles per hour. On the second day, they traveled the remaining 25% of the distance at 25 miles per hour. Find the average rate of speed for the entire two-day trip. (62.5 miles per hour)

Simplifying Complex Rational Expressions

Lesson Plan