• Think-Pair-Share activity
• Teacher observations during group activities and class discussion
• Exit Ticket activity

T:  Use the following strategies to tailor the lesson to meet the needs of your students throughout the year.

Routine: Group and partner work is used throughout so that students can help each other. Emphasis should be placed on communicating mathematical ideas with the specific vocabulary words appropriate to the concepts. Encourage students to create and explain real-world contexts for different graphs and equations used in the problems.

Partner and Small-Group Activity (Visual):

Place students in pairs. Give each pair a poster-sized piece of graph paper that already has the x- and y-axes drawn as well as two equations written at the top. In addition, give students sticky dots (five in two different colors and one in a third color), two pieces of string and tape.

1. Student A plots five points for the first equation, and Student B plots five points for the second equation.
2. If there are two sticky dots on the same point, students place the third colored dot on that intersection point.
3. Students should tape the string on the graph to represent the lines.
4. If students plot points that don’t overlap, they must figure out what the coordinates are for the point where the two strings intersect.
5. Students substitute the x and y-values of the shared point to prove that the point satisfies both equations and is therefore the true intersection point of the graphs.

Technology Connection: Have students explore systems of equations with nonintegral solutions using graphing calculators or software.

O: This lesson uses a competition context to keep students engaged while they explore systems of equations. Students review how to graph linear functions. The focus is placed on interpreting the meaning of the points of intersection as a solution. Students discover the connection between systems of equations and real-world situations.

W: After this lesson, students will understand that the solution to a system of equations represents the point where the graphs of the two lines intersect. Students are learning how to solve a system of equations because there are many real-world situations modeled by linear equations involving different rates of change. Students will be able to solve a system of equations by graphing the lines of the two equations. They will be able to check their work by substituting the coordinates of the intersection point into both equations to illustrate that the intersection point satisfies both equations.

H:  Think-Pair-Share

Use the following scenario to set up a real-world situation involving a system of linear equations. “With your partner, think about a school recycling competition. Two classes are competing in a recycling competition; one class collected three-quarters of a pound of cans each day. The other class knew about the competition ahead of time and started with two pounds but collected one quarter-pound each day. With your partner figure out when the first class will pass the second class in terms of total pounds of weight collected.” Students may use multiple methods; most will likely use a guess-and- check method. Ask pairs to present their answers (4 days is the correct answer). Have students share the different methods they used to solve the problem.

“Could we write equations that model the class can-collection scenarios?”

Review how to write a linear equation.  [IS.3 - All Students]
Define the variables: x = number of days, y = weight of cans (lbs.)

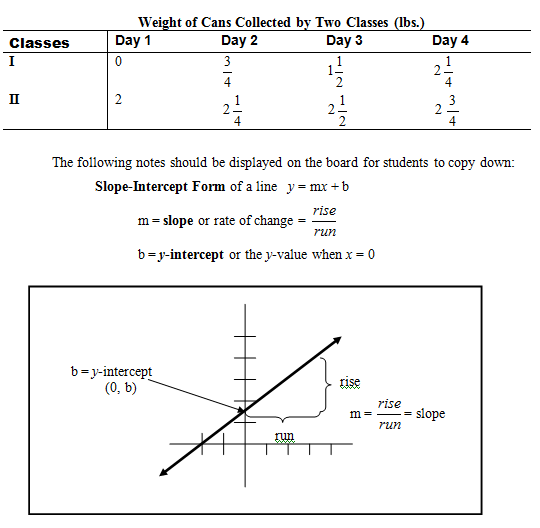
Create small groups combining pairs of students. Give each group graph paper and markers. Have each group agree on two equations they discovered in the previous activity. Ask them to graph both lines on the same grid. (If any pairs of students used this method to solve the previous equation, have them walk around and help other students who are struggling with either the equation or the graphing).   

      After students are finished with their graphs, display the two graphed equations on a transparency overhead, poster sized graph paper or smart board.

“What do you notice about the two graphs?” Students should respond that the two graphs intersect at the same place as the answer.

“What is the meaning of the intersection point (4, 3)?” Students should be able to explain that the coordinate pair represents the fact that both classes will have three pounds of cans in four days. It also indicates a critical point of change in the data, where the team that was behind has caught up and will stay ahead of the previous leader.

     “When there is more than one equation on a grid, it is called a system of equations. The solution to the system is where the lines intersect.”

 “A system of equations is a set or collection of equations that contain the same variables. Systems are sometimes denoted with a brace:

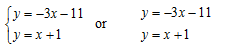
The x and y values that satisfy both equations are known as the solution to the system and are represented by the point where the two lines intersect.”

Activity 1 (Kinesthetic): The Human Graph [IS.4 - All Students]

Take students to a large area (hallway, cafeteria, gym, large classroom, outside) and split into groups. The ideal group size is ten students. Eight students are going to be human coordinates (four per equation) and the other two are going to be drawing the graphs on paper as a way to record the group’s work. Each group should have two long ropes and two long strings. The long ropes should have tape markers at one foot intervals. Place the ropes on the ground for the x- and y-axes.

1. Give the groups two equations. Example: y = –4x – 2 and y = –3x – 1.
2. Four students represent four points on the graph of the first equation, and four students represent four points on the graph for the second equation. Tell them to use the same x-coordinates.
3. When each group of four is “graphed,” they will use the string to connect themselves to form two straight lines.
4. The recorders will draw the graph of the equation for their group. One student graphs the line of y = –4x – 2 and the other student graphs

y = –3x – 1 on the same sheet of paper using the same coordinate grid.

1. Ask the group to write down their observations of the two lines. Students representing the line stay in their graph formation while the two student recorders who drew the graphs write down what their group members say in response to the following questions: 

• “Are the lines going in the same direction?”
• “What is the slope and y-intercept for each equation?”
• “Are there two students standing on the same point?”
• “If so, what do you think this means?”
• “What are the coordinates of that shared point?”

1. If there is time, the group should do another system of equations and change roles so there is a new recorder.
2. When all of the groups are finished, go back to the classroom and discuss what it means for two students to be standing on the same point when they represent a point on two different equations.
3. After the discussion, tell students to substitute the x-value of the shared point into both equations and ask what they get for an answer.

“What does that point mean in terms of the graphs of the equations?”

      Activity 2 (Auditory/Visual)

Each student should have graph paper and a ruler (this is an individual activity). You will read two equations. Example: y = 2x – 5 and y = -x + 7 Have students graph both lines on the same coordinate grid and determine where the lines intersect. When they are done with the graph, ask students to show their work algebraically by replacing the x- and y-values into both equations, to check that the coordinate pair satisfies both equations. Repeat this activity with different linear systems. Emphasize to students that the solution to the system (or the coordinates of the shared point) is where the two lines intersect.

Activity 3: Parallel and Concurrent Lines

Prepare a display-size chart or large Post-It with a coordinate grid containing at least 15 horizontal and vertical units in both directions from the origin. Prepare three different colored, similar right triangles with integer bases and altitudes that correspond to the units on the display grid.

Cut these assorted right triangles from construction paper. For example, similar right triangles with base 5 units and altitude 2 units are similar to those with bases of 10, 15, 20, … and altitudes 4, 6, 8, … respectively. Since the hypotenuses of all of these similar right triangles have the same slope (when in the same orientation), each hypotenuse is parallel to each other hypotenuse. Similarly, when the hypotenuse of any of the similar right triangles intersects the y-axis at (0, 9) with its altitude parallel to the y-axis and base parallel to the x-axis, the hypotenuses are concurrent.

1. Cut out one right triangle with a base 10 units and altitude 4 units; a second right triangle of a different color with base 5 units and altitude 2 units; and a third right triangle of another different color with base 15 units and altitude 6 units.
2. On the grid, mark the ordered pairs (0, 5), (0, 9) and (10, 5). Place the first right triangle on the grid with the vertex of its right angle on (0, 5) and the vertex of its smallest angle on (10, 5). Lightly tape the triangle in position to the grid. Point out to the students that its current orientation has the slope of the hypotenuse in a negative direction (upper left to lower right).
3. Ask one student to position the larger right triangle on the grid with its altitude parallel to the y-axis, base parallel to the x-axis, and the vertex of its smallest angle to the right. Have the student move the triangle to other locations on the grid in the same orientation and point out the necessity of its hypotenuse remaining parallel to the first triangle as long as its x- and y-axis orientation remains the same.

R Activity 4 [IS.5 - All Students]

E:  An exit ticket (A1-5-1_Exit Ticket.docx) is a quick way to evaluate whether students understand the concepts. Bring back the discussion from the beginning of class regarding the recycling competition. Introduce a new scenario: “Our class is going to have a fundraiser that is a walking competition with the principal around the school’s track. We will give the principal a two-mile lead, and she walks three-quarters of a mile per hour. The student representing our class walks 2.5 miles per hour.” On a sheet of graph paper, have students perform the following:

1.  Write the two equations for the given scenario.
2. Graph both lines, labeling the axes, the y-intercepts and the point of intersection.
3. Substitute the x- and y-values of the intersection point into the equations to show that the point satisfies both equations.
4. Explain what the intersection point means in terms of the walking competition.